Coding Interview Questions - Pattern 1 - Tries (Prefix Trees)

Trie is a must learn data structure for top tech company interviews.

One of the most frequently asked coding interview questions for FAANG companies [Facebook (FB), Amazon (AMZN), Apple (AAPL), Netflix (NFLX); and Alphabet (GOOG) (formerly known as Google).] include Tries. Trie has multiple variants. But its very important to learn the data structure before going to onsite interviews. Lets get into the details of it.

Top Interview Questions related to trie (Must Learn) include:

Implement Trie Datastructure

Desing Search Autocomplete

Practical Application - Search Engine Auto Suggestion:

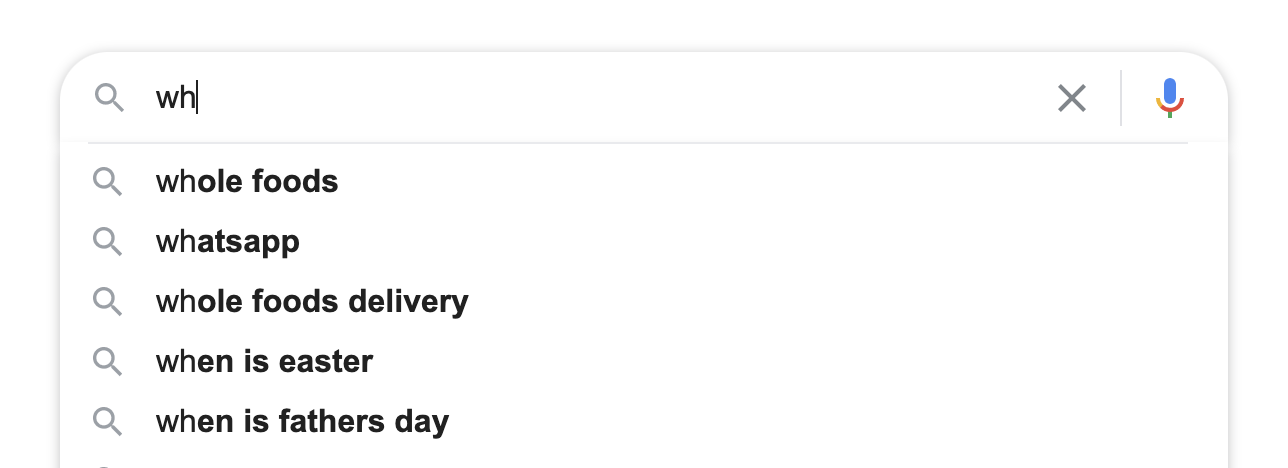
Consider a search engine which does Auto suggestion. As seen in the image above, the moment we start typing the words like ‘wh’, we see sentence suggestions pop up based on the letters that are typed eg: whole foods, whatsapp etc. All these suggested sentences begin with the letters ‘wh’ . As we type more letters, all relevant suggestions help us lead to make our search faster.
If we have to implement this kind of functionality, Brute force approach of storing all the sentences and iterating them to match the sentence prefixes with the letters typed would not help at scale.
Trie is the best data structure to use in this kind of scenarios.

What is a Trie?

Trie (also called as prefix tree) is a kind of search tree, where each node holds

1. A map of all the children with key : Next character, Value : Next character’s node. Reason that children are mapped as map is that the lookup can be faster using the starting character instead of a list.
2. A boolean whether the current node is a leaf or not.

1
2
3
4
class TrieNode {
    Map<Character, TrieNode> childMap;
    boolean amILeaf;
}

Sample Model:

Consider the example sentences as “what”, “whatsapp”, “whole”, “whole foods” These sentences can be represented in the trie format as below:

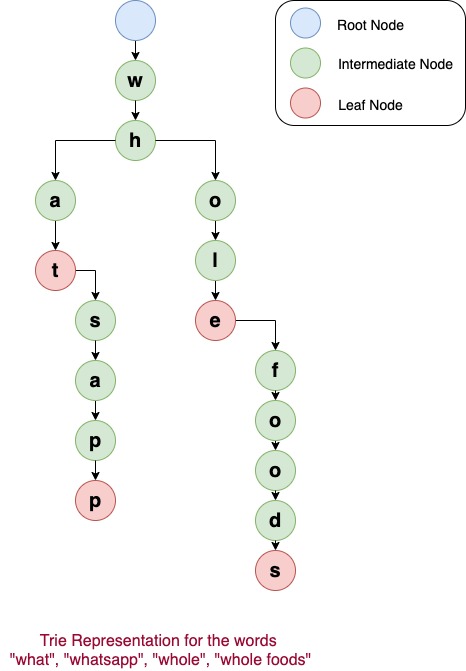
Sample WordList: “what”, “whatsapp”, “whole”, “whole foods”

Root node in a trie is always empty. So blue node in the picture above is empty. But it can have multiple children.
As we can see from the trie representation, since all the sample words start with the same letter ‘w’, the root node (in blue) has only one child with Node(‘w’). Node ‘w’ has one child node ‘h’ since all the words start with ‘wh’. Node(‘h’) has two children nodes Node (‘a’) and Node(‘o’) because the words can be started with ‘wha’ or ‘who’. Similarly words starting with ‘wha’ have ‘t’ as the next character. So only Node(‘t’) is the child of Node(‘a’).. As we reach Node(‘t’), we see that ‘what’ is actually part of the sample word list. So Node (‘t’) is marked as leaf node with the boolean varilable amILeaf as true. Also Node(‘t’) has one possible next character as ‘s’ from the word (‘whatsapp’). So it has one child Node (‘s’) and the whole structure continues until all the words are covered as part of the leaf nodes.

Construction/Insertion of Nodes: We construct the Trie by iterating each of the input words one by one. Each character of the input word is taken and the relationships are formed. For the sample list : “what”, “whatsapp”, “whole”, “whole foods”, Each word is iterated and inserted into the trie with the below code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class TrieNode {
    Map<Character, TrieNode> childMap;
    boolean amILeaf;
}

/** Inserts a word into the trie. */
public void insert(TrieNode root, String word) {

    TrieNode node = root;
    for(char w : word.toCharArray()) {
        if(node.map.get(w) == null) {
            TrieNode child = new TrieNode();
            node.map.put(w, child);
        }
        node = node.map.get(w);
        //node reference changed to current node. 
    }
    
    node.isLeaf = true;
}

For word “what” , ‘w’, ‘h’, ‘a’, ‘t’ are inserted character by character. From the childMap of root ‘w’ is queried. If its empty , new TrieNode child is created and inserted into the root map. If the node already exists, next character continues by assigning node with the current character. If there are no more characters left, then the node is marked as a leaf
Same process continues for all the remaining words.

Time complexity : O(m), where m is the word length. In each iteration of the algorithm, we either examine or create a node in the trie till we reach the end of the word.

Space complexity : O(m). In the worst case newly inserted key doesn’t share a prefix with the the keys already inserted in the trie. We have to add mm new nodes, which takes us O(m) space.

Search:

1
2
3
4
5
6
7
8
9
10
11
12
13
/** Returns if the word is in the trie. */
public boolean search(TrieNode root, String word) {
    Trie node = root;
    for(char ch : word.toCharArray()) {
        if(node.map.get(ch) == null) {
            return false;
        }
        node = node.map.get(ch);
    }
    
    return node.isLeaf;   
}
    

Search follows similar logic as insert. Each character of the word to be search is iterated and node is traversed one by one from the root. If at any instance, there is no node with the character of the search word, it means the word is not present in the word list.

Time Complexity: O(m) : m is the length of the word to be searched. Space Complexity: O(1)

Similar approach can be applied to the Auto Suggestion problem. Initially a trie is constructed with all the possible sentences. For the given input word , it can query the trie for all the words matched the searched prefix.