1
2
3
4
5
6
7
8
9
10
11
12
13
| def fn(arr):
left = ans = 0
right = len(arr) - 1
while left < right:
# do some logic here with left and right
if CONDITION:
left += 1
else:
right -= 1
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| def fn(arr1, arr2):
i = j = ans = 0
while i < len(arr1) and j < len(arr2):
# do some logic here
if CONDITION:
i += 1
else:
j += 1
while i < len(arr1):
# do logic
i += 1
while j < len(arr2):
# do logic
j += 1
return ans
|
Sliding window
1
2
3
4
5
6
7
8
9
10
11
12
13
| def fn(arr):
left = ans = curr = 0
for right in range(len(arr)):
# do logic here to add arr[right] to curr
while WINDOW_CONDITION_BROKEN:
# remove arr[left] from curr
left += 1
# update ans
return ans
|
Build a prefix sum
1
2
3
4
5
6
| def fn(arr):
prefix = [arr[0]]
for i in range(1, len(arr)):
prefix.append(prefix[-1] + arr[i])
return prefix
|
Efficient string building
1
2
3
4
5
6
7
| # arr is a list of characters
def fn(arr):
ans = []
for c in arr:
ans.append(c)
return "".join(ans)
|
In JavaScript, benchmarking shows that concatenation with += is faster than using .join().
Linked list: fast and slow pointer
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int fn(ListNode head) {
def fn(head):
slow = head
fast = head
ans = 0
while fast and fast.next:
# do logic
slow = slow.next
fast = fast.next.next
return ans
}
|
Reversing a linked list
1
2
3
4
5
6
7
8
9
10
| def fn(head):
curr = head
prev = None
while curr:
next_node = curr.next
curr.next = prev
prev = curr
curr = next_node
return prev
|
Find number of subarrays that fit an exact criteria
1
2
3
4
5
6
7
8
9
10
11
12
13
| from collections import defaultdict
def fn(arr, k):
counts = defaultdict(int)
counts[0] = 1
ans = curr = 0
for num in arr:
# do logic to change curr
ans += counts[curr - k]
counts[curr] += 1
return ans
|
Monotonic increasing stack
The same logic can be applied to maintain a monotonic queue.
1
2
3
4
5
6
7
8
9
10
11
12
| def fn(arr):
stack = []
ans = 0
for num in arr:
# for monotonic decreasing, just flip the > to <
while stack and stack[-1] > num:
# do logic
stack.pop()
stack.append(num)
return ans
|
Binary tree: DFS (recursive)
1
2
3
4
5
6
7
8
9
10
| def dfs(root):
if not root:
return
ans = 0
# do logic
dfs(root.left)
dfs(root.right)
return ans
|
Binary tree: DFS (iterative)
1
2
3
4
5
6
7
8
9
10
11
12
13
| def dfs(root):
stack = [root]
ans = 0
while stack:
node = stack.pop()
# do logic
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return ans
|
Binary tree: BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| from collections import deque
def fn(root):
queue = deque([root])
ans = 0
while queue:
current_length = len(queue)
# do logic for current level
for _ in range(current_length):
node = queue.popleft()
# do logic
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return ans
|
Graph: DFS (recursive)
For the graph templates, assume the nodes are numbered from 0 to n - 1 and the graph is given as an adjacency list. Depending on the problem, you may need to convert the input into an equivalent adjacency list before using the templates.
1
2
3
4
5
6
7
8
9
10
11
12
13
| def fn(graph):
def dfs(node):
ans = 0
# do some logic
for neighbor in graph[node]:
if neighbor not in seen:
seen.add(neighbor)
ans += dfs(neighbor)
return ans
seen = {START_NODE}
return dfs(START_NODE)
|
Graph: DFS (iterative)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| def fn(graph):
stack = [START_NODE]
seen = {START_NODE}
ans = 0
while stack:
node = stack.pop()
# do some logic
for neighbor in graph[node]:
if neighbor not in seen:
seen.add(neighbor)
stack.append(neighbor)
return ans
|
Graph: BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| from collections import deque
def fn(graph):
queue = deque([START_NODE])
seen = {START_NODE}
ans = 0
while queue:
node = queue.popleft()
# do some logic
for neighbor in graph[node]:
if neighbor not in seen:
seen.add(neighbor)
queue.append(neighbor)
return ans
|
Find top k elements with heap
1
2
3
4
5
6
7
8
9
10
11
| import heapq
def fn(arr, k):
heap = []
for num in arr:
# do some logic to push onto heap according to problem's criteria
heapq.heappush(heap, (CRITERIA, num))
if len(heap) > k:
heapq.heappop(heap)
return [num for num in heap]
|
Binary search
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def fn(arr, target):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
# do something
return
if arr[mid] > target:
right = mid - 1
else:
left = mid + 1
# left is the insertion point
return left
|
Binary search: duplicate elements, left-most insertion point
1
2
3
4
5
6
7
8
9
10
11
| def fn(arr, target):
left = 0
right = len(arr)
while left < right:
mid = (left + right) // 2
if arr[mid] >= target:
right = mid
else:
left = mid + 1
return left
|
Binary search: duplicate elements, right-most insertion point
1
2
3
4
5
6
7
8
9
10
11
| def fn(arr, target):
left = 0
right = len(arr)
while left < right:
mid = (left + right) // 2
if arr[mid] > target:
right = mid
else:
left = mid + 1
return left
|
Binary search: for greedy problems
If looking for a minimum:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def fn(arr):
def check(x):
# this function is implemented depending on the problem
return BOOLEAN
left = MINIMUM_POSSIBLE_ANSWER
right = MAXIMUM_POSSIBLE_ANSWER
while left <= right:
mid = (left + right) // 2
if check(mid):
right = mid - 1
else:
left = mid + 1
return left
|
If looking for a maximum:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def fn(arr):
def check(x):
# this function is implemented depending on the problem
return BOOLEAN
left = MINIMUM_POSSIBLE_ANSWER
right = MAXIMUM_POSSIBLE_ANSWER
while left <= right:
mid = (left + right) // 2
if check(mid):
left = mid + 1
else:
right = mid - 1
return right
|
Backtracking
1
2
3
4
5
6
7
8
9
10
11
12
| def backtrack(curr, OTHER_ARGUMENTS...):
if (BASE_CASE):
# modify the answer
return
ans = 0
for (ITERATE_OVER_INPUT):
# modify the current state
ans += backtrack(curr, OTHER_ARGUMENTS...)
# undo the modification of the current state
return ans
|
Dynamic programming: top-down memoization
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| def fn(arr):
def dp(STATE):
if BASE_CASE:
return 0
if STATE in memo:
return memo[STATE]
ans = RECURRENCE_RELATION(STATE)
memo[STATE] = ans
return ans
memo = {}
return dp(STATE_FOR_WHOLE_INPUT)
|
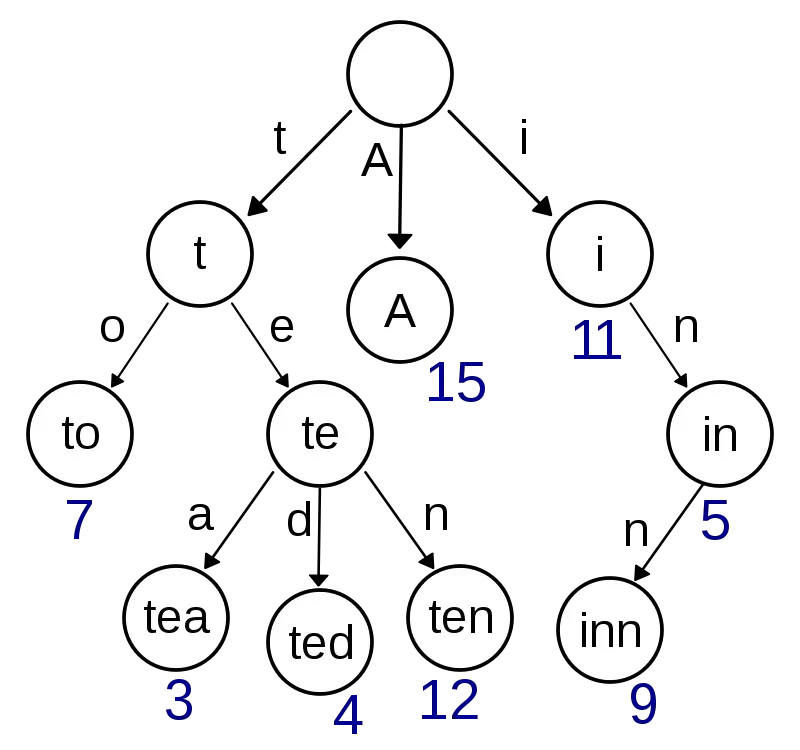
Build a trie
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| # note: using a class is only necessary if you want to store data at each node.
# otherwise, you can implement a trie using only hash maps.
class TrieNode:
def __init__(self):
# you can store data at nodes if you wish
self.data = None
self.children = {}
def fn(words):
root = TrieNode()
for word in words:
curr = root
for c in word:
if c not in curr.children:
curr.children[c] = TrieNode()
curr = curr.children[c]
# at this point, you have a full word at curr
# you can perform more logic here to give curr an attribute if you want
return root
|
We hope you like this post. If you have any questions or suggestions or need any other additional info, please comment below.
We have started a coding community for most frequently used real world coding tips. You can join us here
What do you want to learn next ? Drop a comment below!