Given a rows x cols matrix grid representing a field of cherries. Each cell in grid represents the number of cherries that you can collect.
You have two robots that can collect cherries for you, Robot #1 is located at the top-left corner (0,0) , and Robot #2 is located at the top-right corner (0, cols-1) of the grid.
Return the maximum number of cherries collection using both robots by following the rules below:
- From a cell (i,j), robots can move to cell (i+1, j-1) , (i+1, j) or (i+1, j+1).
- When any robot is passing through a cell, It picks it up all cherries, and the cell becomes an empty cell (0).
- When both robots stay on the same cell, only one of them takes the cherries.
- Both robots cannot move outside of the grid at any moment.
- Both robots should reach the bottom row in the
grid.
Example 1:
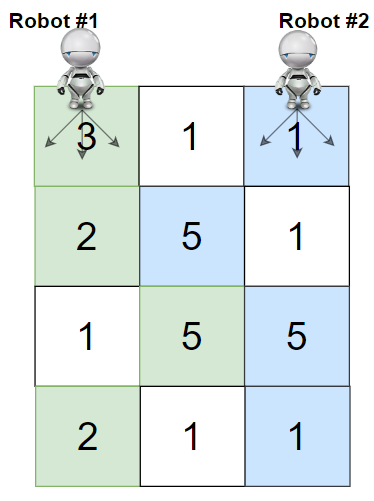
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]] Output: 24 Explanation: Path of robot #1 and #2 are described in color green and blue respectively. Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12. Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12. Total of cherries: 12 + 12 = 24.
Example 2:
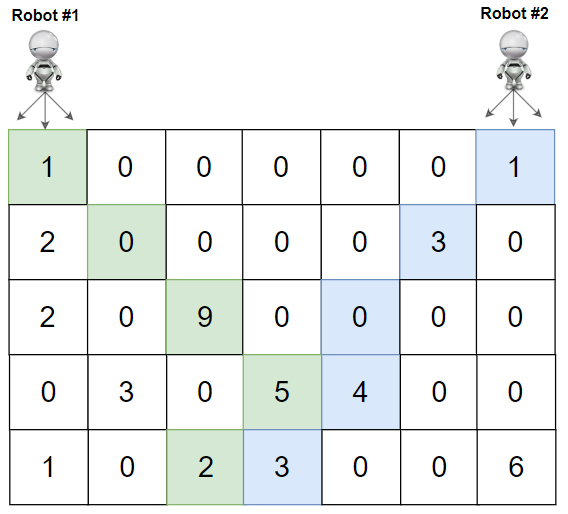
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]] Output: 28 Explanation: Path of robot #1 and #2 are described in color green and blue respectively. Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17. Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11. Total of cherries: 17 + 11 = 28.
Example 3:
Input: grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]] Output: 22
Example 4:
Input: grid = [[1,1],[1,1]] Output: 4
Constraints:
rows == grid.lengthcols == grid[i].length2 <= rows, cols <= 700 <= grid[i][j] <= 100
Solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
* Time Complexity: O(M * N ^ 2)
* Space Complexity: O(M * N ^ 2)
**/
class Solution {
public int cherryPickup(int[][] grid) {
dp = new int[grid.length][grid[0].length][grid[0].length];
for (int i = 0; i < dp.length; i++) {
for (int j = 0; j < dp[i].length; j++) {
Arrays.fill(dp[i][j], -1);
}
}
return solve(grid, 0, 0, grid[0].length - 1);
}
int[][][] dp;
int solve(int[][] grid, int x, int y1, int y2) {
if (x < 0 || x >= grid.length || y1 < 0 || y1 >= grid[0].length || y2 < 0 || y2 >= grid[0].length) {
return 0;
}
if (dp[x][y1][y2] != -1) {
return dp[x][y1][y2];
}
int res = grid[x][y1];
if (y1 != y2) {
res += grid[x][y2];
}
int max = Integer.MIN_VALUE;
for (int i = -1; i <= 1; i++) {
for (int j = -1; j <= 1; j++) {
max = Math.max(max, solve(grid, x + 1, y1 + i, y2 + j));
}
}
res = res + max;
dp[x][y1][y2] = res;
return res;
}
}