There is an undirected graph with n nodes, where each node is numbered between
0 and n - 1. You are given a 2D array graph, where graph[u] is
an array of nodes that node u is adjacent to. More formally, for each v in
graph[u], there is an undirected edge between node u and node v. The graph
has the following properties:
- There are no self-edges (
graph[u]does not containu). - There are no parallel edges (
graph[u]does not contain duplicate values). - If
vis ingraph[u], thenuis ingraph[v](the graph is undirected). - The graph may not be connected, meaning there may be two nodes
uandvsuch that there is no path between them.
A graph is bipartite if the nodes can be partitioned into two independent sets A
and B such that every edge in the graph connects a node in set A and
a node in set B.
Return true if and only if it is bipartite.
Example 1:
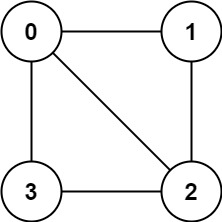
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]] Output: false Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2:
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
graph.length == n1 <= n <= 1000 <= graph[u].length < n0 <= graph[u][i] <= n - 1graph[u]does not containu.- All the values of
graph[u]are unique. - If
graph[u]containsv, thengraph[v]containsu.
Solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
* Intuition: Each node is seperated into two different parties (0, 1). We do a dfs to distinguish the parties.
* If at any moment, we find the party of two adjacent nodes is same, it means we can't divide the graph
* into two different parties. Since there could be interdepency.
* <p>
* So we do a DFS + Party Map.
* Time Complexity: O(N+E) : N is the number of nodes in graph, E is the number of edges
* Space Complexity: O(N)
**/
class Solution {
public boolean isBipartite(int[][] graph) {
Set<Integer> visited = new HashSet<>();
for (int i = 0; i < graph.length; i++) {
dfs(graph, i, visited, new HashMap<>());
if (!res) {
return res;
}
}
return true;
}
boolean res = true;
void dfs(int[][] graph, int i, Set<Integer> visited, Map<Integer, Integer> party) {
if (visited.contains(i)) {
return;
}
visited.add(i);
for (int j = 0; j < graph[i].length; j++) {
int x = i;
int y = graph[i][j];
Integer a = party.get(x);
Integer b = party.get(y);
if (a == null && b == null) {
party.put(x, 0);
party.put(y, 1);
} else if (a == null && b != null) {
party.put(x, (b + 1) % 2);
} else if (a != null && b == null) {
party.put(y, (a + 1) % 2);
} else if (a != null && b != null) {
if (a.equals(b)) {
res = false;
return;
}
}
dfs(graph, y, visited, party);
}
}
}